In modern portfolio theory, the risk parity (RP) strategy has established itself as an alternative to traditional Markowitz mean-variance optimization (MV), particularly in the area of systematic multi-asset allocation. This strategy distributes risk evenly across assets instead of allocating capital proportionally. More specifically, each asset should contribute equally to the overall portfolio risk. A new publication by Dr. Patrick Walker (Head of Investment Solutions, OLZ AG) together with researchers from the University of Zurich and Stony Brook University in New York in the renowned Journal of Time Series Analysis examines RP optimization using expected shortfall (also known as conditional value at risk, or CVaR) instead of volatility as a measure of risk. In order to enable the most realistic modeling of financial market risks possible, leptokurtic ("fat-tailed") and heteroscedastic returns are linked to a model for dynamic correlations. This allows both extreme events that are not adequately described by a normal distribution to be taken into account and the risk and dependency structures between assets that change over time to be mapped. This advanced modeling approach enables both efficient parameter estimation and simplified calculation of the risk contributions of each asset in the portfolio. As a result, RP optimization can be solved quickly and accurately, despite a significantly more flexible and realistic model for the return time series.
Overcoming the weaknesses of traditional portfolio optimization
Classic MV optimization in its original form suffers from high sensitivity to estimation errors, especially in expected returns, which can lead to unstable portfolio weightings and poor performance in practice. One approach to overcoming these problems is to focus on the minimum variance portfolio and further improve its quality using modern statistical methods such as shrinkage estimation or regularization. Another approach that also focuses exclusively on risk distribution but pursues a different objective function is the RP portfolio. Despite the high importance of realistic risk modeling, standard RP implementations are based on the assumption of normally distributed returns whose parameters do not change over time. However, this obviously does not do justice to real financial markets, as returns often have strong outliers (extreme events) and volatilities and correlations can change rapidly, especially in times of crisis.
The role of generalized hyperbolic distributions
To better model real return characteristics, the study uses an elliptical multivariate generalized hyperbolic distribution. This distribution class allows for better mapping of particularly large price jumps in periods of high volatility, while at the same time enabling rapid estimation of parameters using so-called EM algorithms. A key innovation of the work is the derivation of a semi-closed formula for risk contributions using CVaR as a risk measure, which eliminates the need for computationally intensive simulations.
Improvement of RP optimization with dynamic correlations
Another significant contribution is the integration of a multivariate GARCH model with dynamic, regime-dependent correlations. Market conditions fluctuate between different correlation regimes, particularly between calm market phases and bear markets. By taking dynamic correlations into account, risk dependencies are better captured over time, resulting in more robust portfolio allocations.
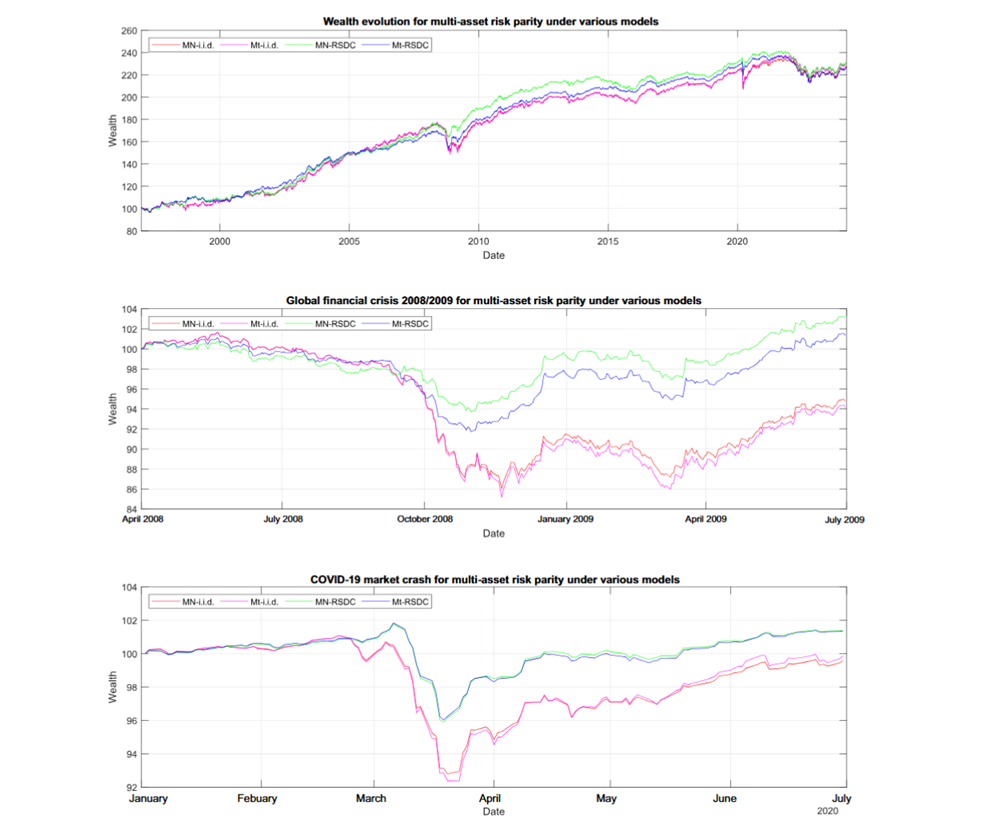
Empirical findings: Improved stability and lower portfolio turnover
The empirical analysis covers several periods of sharply increased market risk, including the 2008 global financial crisis and the COVID-19 crash. The key findings include:
Lower portfolio turnover: Models with fat-tailed distributions lead to smoother portfolio adjustments as they absorb market shocks more effectively. This is particularly relevant during times of crisis when volatility spikes and unnecessary trading activity due to increased bid-ask spreads must be avoided.
Improved risk-adjusted returns: RP portfolios using the time series model described achieved higher Sharpe and Sortino ratios compared to normally distributed and static models.
Better control of extreme risk: RP portfolios based on expected shortfall showed greater resilience in periods of extreme market turbulence and are therefore particularly suitable for risk-averse investors.